The Icosahedral Equation

The Icosahedral Equation#

By now, it should be clear that — given an arbitrary quintic equation — it’s possible to massage this quintic into a form that can be used to easily determine the roots: first one passes from the general quintic to a corresponding “principal quintic” with roots given by

y_{r} = \frac{W_{r} (z_{0}, 1) f (z_{0}, 1)}{H (z_{0}, 1)} (λ_{\pm} + μ_{\pm} \frac{t_{r} (z_{0}, 1) f^{2} (z_{0}, 1)}{T (z_{0}, 1)}) .

where $λ_{\pm}$ , $μ_{\pm}$ are determined in terms of the coefficients of the principal quintic. Once these roots are computed, the corresponding roots of the general quintic are found by solving one last quadratic equation:

y_{r} = x_{r}^{2} + A x_{r} + B_{\pm}

for some $A (p_{i})$ , $B_{\pm} (p_{i})$ which determine the principal quintic, given the coefficients $p_{i}$ of the original quintic.

from sympy import Function, symbols

a, b, c, z = symbols("a b c z")

f = Function("f")
g = Function("g")
phi = Function("phi")

from sympy import diff, dsolve

result = dsolve(2 * diff(phi(z), z) + (c - (a + b + 1) * z) / z / (1 - z), phi(z))

result.rhs

C_{1} - \frac{c \log (z)}{2} - \frac{(a + b - c + 1) \log (z - 1)}{2}

from sympy import simplify

expr = (
    z * (1 - z) * (diff(phi(z), z, z) + diff(phi(z), z) ** 2)
    + diff(phi(z), z) * (c - (a + b + 1) * z)
    - a * b
)
simplify(expr.subs(phi(z), result.rhs).doit()).factor()

\frac{a^{2} z^{2} - 2 a b z^{2} + 4 a b z - 2 a c z + b^{2} z^{2} - 2 b c z + c^{2} + 2 c z - 2 c - z^{2}}{4 z (z - 1)}

from sympy import exp

hypergeom = (
    diff(f(z), z, z)
    + (c - (a + b + 1) * z) / z / (1 - z) * diff(f(z), z)
    - a * b * f(z) / z / (1 - z)
)
diffterm = hypergeom.subs(f(z), exp(phi(z)) * g(z)).doit().expand().coeff(
    diff(g(z), z)
) / exp(phi(z))
simplify(diffterm)

\frac{a z + b z - c + 2 z (z - 1) \frac{d}{d z} ϕ (z) + z}{z (z - 1)}

hypergeom

- \frac{a b f (z)}{z (1 - z)} + \frac{d^{2}}{d z^{2}} f (z) + \frac{(c - z (a + b + 1)) \frac{d}{d z} f (z)}{z (1 - z)}

result = dsolve(diffterm, phi(z))
result.rhs

C_{1} - \frac{c \log (z)}{2} - \frac{(a + b - c + 1) \log (z - 1)}{2}

expr2 = simplify(
    hypergeom.subs(f(z), exp(result.rhs) * g(z)).doit() / exp(result.rhs)
).expand()
expr2

- \frac{a^{2} z^{2} g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} + \frac{2 a b z^{2} g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} - \frac{4 a b z g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} + \frac{2 a c z g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} - \frac{b^{2} z^{2} g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} + \frac{2 b c z g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} - \frac{c^{2} g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} - \frac{2 c z g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} + \frac{2 c g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} + \frac{4 z^{4} \frac{d^{2}}{d z^{2}} g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} - \frac{8 z^{3} \frac{d^{2}}{d z^{2}} g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} + \frac{z^{2} g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}} + \frac{4 z^{2} \frac{d^{2}}{d z^{2}} g (z)}{4 z^{4} - 8 z^{3} + 4 z^{2}}

simplify(expr2.coeff(diff(g(z), z, z)))

1

from sympy import fraction

simplify(expr2.coeff(g(z))).factor()
num, denom = fraction(_)
num

1

denom

1

num.collect(z)

1

num.collect(a)

1

num.collect(c)

1

from sympy import Eq, Rational, hyper, oo, real_root, solve

w = symbols("w")


def get_soln(sg1, sg2, sg3, exp_pt):
    a, b, c = symbols("a b c")
    eq1 = Eq(c - a - b, sg1 * Rational(1, 2))
    eq2 = Eq(1 - c, sg2 * Rational(1, 3))
    eq3 = Eq(a - b, sg3 * Rational(1, 5))
    solns = solve([eq1, eq2, eq3], [a, b, c])
    a = solns[a]
    b = solns[b]
    c = solns[c]
    coeff = 1 / real_root(1728, 5)
    print(a, b, c)
    if exp_pt == 0:
        return (
            lambda z: coeff
            * hyper([a, b], [c], z)
            / (z ** (1 - c) * hyper([1 + a - c, 1 + b - c], [2 - c], z))
        )
    elif exp_pt == 1:
        num = lambda z: hyper([a, b], [1 + a + b - c], 1 - z)
        denom = lambda z: (1 - z) ** (c - a - b) * hyper(
            [c - a, c - b], [1 + c - a - b], 1 - z
        )
        return lambda z: coeff * num(z) / denom(z)
    elif exp_pt == oo:
        num = lambda z: z ** (-a) * hyper([a, 1 + a - c], [1 + a - b], 1 / z)
        denom = lambda z: z ** (-b) * hyper([b, 1 + b - c], [1 + b - a], 1 / z)
        return lambda z: coeff * num(z) / denom(z)
        # if z == oo:
        #     num = lambda w: (1 / w) ** (-a) * hyper([a, 1 + a - c], [1 + a - b], w)
        #     denom = lambda w: (1 / w) ** (-b) * hyper([b, 1 + b - c], [1 + b - a], w)
        #     return lambda z: coeff * limit(num(w) / denom(w), w, 1 / z)
        # elif z == 0:
        #     print("here")
        #     num = lambda z: z ** (-a) * hyper([a, 1 + a - c], [1 + a - b], 1 / z)
        #     denom = lambda z: z ** (-b) * hyper([b, 1 + b - c], [1 + b - a], 1 / z)
        #     return lambda z: coeff * limit(num(z) / denom(z), z, 0, dir="-")
        # else:
        #     num = lambda z: z ** (-a) * hyper([a, 1 + a - c], [1 + a - b], 1 / z)
        #     denom = lambda z: z ** (-b) * hyper([b, 1 + b - c], [1 + b - a], 1 / z)
        #     return lambda z: coeff * num(z) / denom(z)


get_soln(1, 1, 1, oo)(1).evalf()

11/60 -1/60 2/3

0.284079043840412

get_soln(1, 1, 1, oo)(-0.0000001).evalf()

11/60 -1/60 2/3

0.273111953772192 - 0.198427449322131 i

from itertools import product

for s1, s2, s3, exp_pt in product([+1, -1], [+1, -1], [+1, -1], [0, 1, oo]):
    print(f"{s1, s2, s3, exp_pt}: {get_soln(s1, s2, s3, exp_pt)(-1e-15 * I).evalf()}")

11/60 -1/60 2/3

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[17], line 4
      1 from itertools import product
      3 for s1, s2, s3, exp_pt in product([+1, -1], [+1, -1], [+1, -1], [0, 1, oo]):
----> 4     print(f"{s1, s2, s3, exp_pt}: {get_soln(s1, s2, s3, exp_pt)(-1e-15 * I).evalf()}")

NameError: name 'I' is not defined

for s1, s2, s3 in product([+1, -1], [+1, -1], [+1, -1]):
    print(f"{s1, s2, s3}: {get_soln(s1, s2, s3, 0)(0).evalf()}")

(1, 1, 1): zoo
(1, 1, -1): zoo
(1, -1, 1): 0
(1, -1, -1): 0
(-1, 1, 1): zoo
(-1, 1, -1): zoo
(-1, -1, 1): 0
(-1, -1, -1): 0

for s1, s2, s3 in product([+1, -1], [+1, -1], [+1, -1]):
    print(f"{s1, s2, s3}: {get_soln(s1, s2, s3, 1)(1).evalf()}")

(1, 1, 1): zoo
(1, 1, -1): zoo
(1, -1, 1): zoo
(1, -1, -1): zoo
(-1, 1, 1): 0
(-1, 1, -1): 0
(-1, -1, 1): 0
(-1, -1, -1): 0

for s1, s2, s3 in product([+1, -1], [+1, -1], [+1, -1]):
    print(
        f"{s1, s2, s3}: {get_soln(s1, s2, s3, oo)(-1e-15).doit().evalf()}, {get_soln(s1, s2, s3, oo)(1).evalf()}, {get_soln(s1, s2, s3, oo)(1e55).evalf()}"
    )

(1, 1, 1): 0.273657890659636 - 0.198824095688466*I, 0.284079043840412, 2.25160006420103E-12
(1, 1, -1): 0.121252253496504 + 0.0880949187816968*I, 0.178460993833747, 22516000642.0102
(1, -1, 1): 0.273657890659637 - 0.198824095688467*I, 0.284079043840412, 2.25160006420100E-12
(1, -1, -1): 0.121252253496504 + 0.0880949187816966*I, 0.178460993833747, 22516000642.0104
(-1, 1, 1): 0.273657890659636 - 0.198824095688467*I, oo, 2.25160006420102E-12
(-1, 1, -1): 0.121252253496504 + 0.0880949187816967*I, oo, 22516000642.0103
(-1, -1, 1): 0.273657890659636 - 0.198824095688466*I, oo, 2.25160006420103E-12
(-1, -1, -1): 0.121252253496504 + 0.0880949187816969*I, oo, 22516000642.0101

get_soln(1, 1, 1, oo)(1).evalf()

0.284079043840412

import numpy as np
from matplotlib import pyplot as plt
from sympy import I, pi

thetas = np.linspace(0, 2 * pi, 100, endpoint=False)
vals = []
for theta in thetas:
    val = (
        get_soln(1, 1, 1, oo)(0.00000000001 * exp(I * theta)) * exp(-I * pi / 5)
    ).evalf()
    # print(val)
    if val is not None:
        vals.append(val)
vals = np.array(vals, dtype=np.complex128)
print(vals.dtype)
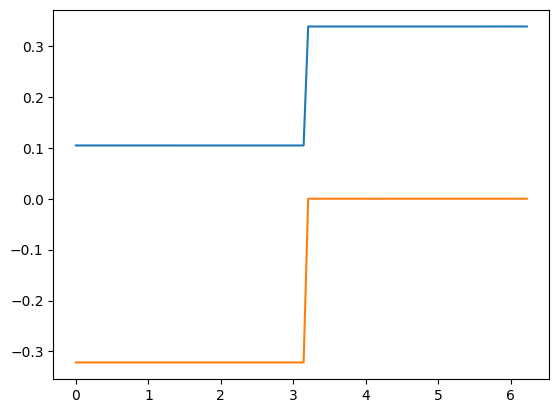
plt.plot(thetas, np.real(vals))
plt.plot(thetas, np.imag(vals))
plt.show()

complex128

_images/25b26e51e32038a87bfdea2eeb4692c00d54eb937d23e321c64537d23f3b7c46.png

import numpy as np
from scipy.special import hyp2f1


def s_inv(Z, sg1=+1, sg2=+1, sg3=+1):
    a, b, c = symbols("a b c")
    eq1 = Eq(c - a - b, sg1 * Rational(1, 2))
    eq2 = Eq(1 - c, sg2 * Rational(1, 3))
    eq3 = Eq(a - b, sg3 * Rational(1, 5))
    solns = solve([eq1, eq2, eq3], [a, b, c])
    a = float(solns[a])
    b = float(solns[b])
    c = float(solns[c])
    # a, b, c = 11 / 60, -1 / 60, 2 / 3
    num = Z ** (-a) * hyp2f1(a, 1 + a - c, 1 + a - b, 1 / Z)
    denom = Z ** (-b) * hyp2f1(b, 1 + b - c, 1 + b - a, 1 / Z)
    # print(num,denom)
    coeff = sg3 / (1728) ** (sg3 / 5)
    # coeff = 1
    # coeff = -3.5201470213402 / 0.7925963259246634
    return coeff * np.divide(num, denom)


s_inv(np.array([-1e-55j])) * np.exp(-np.pi / 5 * 1j)

array([0.33826121-2.50388975e-17j])

from sympy import I, exp, pi

(get_soln(1, 1, 1, oo)(-1e-55 * I) * exp(-I * pi / 5)).evalf()

11/60 -1/60 2/3

0.338261212717716 - 3.3881317890172 \cdot 10^{- 20} i

-((3.5201470213402 / 0.7925963259246634) ** 5)

-1727.9999999999964

If the expansion point is $Z \to \infty$ then we find that first two signs $σ_{1}$ , $σ_{2}$ do not change the resulting expression, but that the sign $σ_{3}$ dictates whether $s (Z \to \infty)$ approaches either 0 ( $σ_{3} = + 1$ ) or $\infty$ ( $σ_{3} = - 1$ ):

s (Z) = \frac{σ_{3}}{(1728)^{\frac{σ_{3}}{5}}} \frac{Z^{- a}_{2} F_{1} (a, 1 + a - c; 1 + a - b; 1 / Z)}{Z^{- b}_{2} F_{1} (b, 1 + b - c; 1 + b - a; 1 / Z)}

As we approach the singular points 0, 1, $\infty$ from above/below the real axis, we find the following:

\begin{cases} ended with \end{split}

Similarly, the other two singular points are found to be

S (0 \pm i ϵ) = σ_{3} (h_{1} e^{\mp i π / 5})^{σ_{3}}, S (1 \pm i ϵ) = z_{n} - σ_{3} j,

where $h_{1} := [(1 - k) z_{n} - 1] / 2 ≃ 0.33826 \dots$ , and where $ϵ > 0$ and $\pm$ dictates whether the singular point is approached from above/below. Since the values in the above with $σ_{3} = + 1$ are antipodal to those with $σ_{3} = - 1$ (and since $z = 0$ is antipodal to $z \to \infty$ ), we find that this sign determines whether the triangle under consideration lies either at the top or the bottom of the Riemann sphere. Lastly, the upper/lower half-planes must describe the mirror image of the fundamental triangle in the $ξ$ -axis, since the vertex and midpoint do not move, as they are real, and the face centre goes from rotated up by $e^{i π / 5}$ to rotated down by the same amount.

1 / 0.3382617

2.9562909427818758

from itertools import product

eps = 1e-55j

for s1, s2, s3 in product([+1, -1], [+1, -1], [+1, -1]):
    print(
        s1,
        s2,
        s3,
        "F:",
        s_inv(eps, sg1=s1, sg2=s2, sg3=s3) * np.exp(-np.pi / 5 * 1j),
        s_inv(eps, sg1=s1, sg2=s2, sg3=s3) * np.exp(+np.pi / 5 * 1j),
        "E:",
        s_inv(1 + eps, sg1=s1, sg2=s2, sg3=s3),
        "V:",
        s_inv(1e55 + eps, sg1=s1, sg2=s2, sg3=s3),
        s_inv(-3 - 5j),
        s_inv(-3 + 5j),
    )

1 1 1 F: (0.1045284632676535-0.3217055305650853j) (0.3382612127177165+2.0165837040625896e-17j) E: (0.2840790438404124-2.0862790179196747e-29j) V: (2.251600064201026e-12-4.503200128402052e-123j) (0.14244767294577834+0.06602319464811653j) (0.14244767294577834-0.06602319464811653j)
1 1 -1 F: (-2.9562952014676105-5.875776049326388e-17j) (-0.9135454576426009-2.811603815447865j) E: (-3.520147021340201-2.585199095058965e-28j) V: (-444128606984.5832-8.882572139691663e-100j) (0.14244767294577834+0.06602319464811653j) (0.14244767294577834-0.06602319464811653j)
1 -1 1 F: (0.10452846326765503-0.32170553056508994j) (0.3382612127177213+3.3086219180672475e-17j) E: (0.2840790438404122-2.0862790179196752e-29j) V: (2.2516000642010035e-12-4.503200128402008e-123j) (0.14244767294577834+0.06602319464811653j) (0.14244767294577834-0.06602319464811653j)
1 -1 -1 F: (-2.9562952014675687+3.0909058052619345e-16j) (-0.9135454576425882-2.811603815447825j) E: (-3.520147021340202-2.5851990950589683e-28j) V: (-444128606984.5877-8.882572139691758e-100j) (0.14244767294577834+0.06602319464811653j) (0.14244767294577834-0.06602319464811653j)
-1 1 1 F: (0.10452846326765271-0.32170553056508305j) (0.3382612127177141-3.936897505271442e-17j) E: (0.2840790438404124+1.2402216765675661e-17j) V: (2.2516000642010184e-12-4.5032001284020385e-123j) (0.14244767294577834+0.06602319464811653j) (0.14244767294577834-0.06602319464811653j)
-1 1 -1 F: (-2.956295201467632-3.537042334655082e-16j) (-0.913545457642607-2.811603815447885j) E: (-3.5201470213402004+1.7059637197440578e-16j) V: (-444128606984.58466-8.882572139691698e-100j) (0.14244767294577834+0.06602319464811653j) (0.14244767294577834-0.06602319464811653j)
-1 -1 1 F: (0.10452846326765282-0.321705530565083j) (0.3382612127177141+7.652638782568283e-17j) E: (0.2840790438404124+2.8171771529931913e-17j) V: (2.2516000642010346e-12-4.503200128402069e-123j) (0.14244767294577834+0.06602319464811653j) (0.14244767294577834-0.06602319464811653j)
-1 -1 -1 F: (-2.956295201467631+5.34474186234617e-16j) (-0.9135454576426076-2.811603815447884j) E: (-3.520147021340201+3.908148273157554e-16j) V: (-444128606984.5815-8.882572139691629e-100j) (0.14244767294577834+0.06602319464811653j) (0.14244767294577834-0.06602319464811653j)

s_inv(-3 - 5j)

np.complex128(0.14244767294577834+0.06602319464811653j)

import numpy as np


def s_inv2(Z, sg1=+1, sg2=+1, sg3=+1):
    a, b, c = symbols("a b c")
    eq1 = Eq(c - a - b, sg1 * Rational(1, 2))
    eq2 = Eq(1 - c, sg2 * Rational(1, 3))
    eq3 = Eq(a - b, sg3 * Rational(1, 5))
    solns = solve([eq1, eq2, eq3], [a, b, c])
    a = float(solns[a])
    b = float(solns[b])
    c = float(solns[c])
    # a, b, c = 11 / 60, -1 / 60, 2 / 3
    num = hyp2f1(a, b, c, Z)
    denom = Z ** (1 - c) * hyp2f1(1 + a - c, 1 + b - c, 2 - c, Z)
    # print(num,denom)
    coeff = 1  # (1728) ** (1 / 5)
    # coeff = 0.284079041754133/0.70882405176421
    # coeff = 0.284079041754133 / 1.4107873420929684
    coeff = 0.338261212717716 / 2.586766338312561
    # coeff = 0.338261212717716 / 0.18448308813935999
    return coeff * np.divide(num, denom)


s_inv2(np.array([-1e-55j]))

array([2.43982662e+17+1.40863456e+17j])

(2.586766338312561 / 0.338261212717716) ** 6

199999.99999279383

0.338261212717716 / 2.586766338312561, 1 / (200000) ** (1 / 6)

(0.13076604860196833, 0.13076604860118307)

(0.284079043840412 / 1.4107873573583158)

0.20136205669743665

(0.338261212717716 / 0.18448308813935999) ** 6

37.99914721467943

from itertools import product

eps = -1e-55j

for s1, s2, s3 in product([+1, -1], [+1, -1], [+1, -1]):
    print(
        s1,
        s2,
        s3,
        "F:",
        s_inv2(eps, sg1=s1, sg2=s2, sg3=s3),
        "E:",
        s_inv2(1 + eps, sg1=s1, sg2=s2, sg3=s3),
        "V:",
        s_inv2(1e55 + eps, sg1=s1, sg2=s2, sg3=s3) * np.exp(-np.pi / 3 * 1j),
        s_inv2(1e55 + eps, sg1=s1, sg2=s2, sg3=s3) * np.exp(+np.pi / 3 * 1j),
    )

1 1 1 F: (2.4398266219041667e+17+1.4086345569323858e+17j) E: (0.09269011940029458+1.0029483789626555e-29j) V: (0.05055193685846039-2.2042011928602662e-13j) (-0.0252759684290393+0.04377926153004382j)
1 1 -1 F: (2.4398266219041667e+17+1.4086345569323858e+17j) E: (0.09269011940029454+1.002948378962655e-29j) V: (0.05055193685846039-2.2042011928602662e-13j) (-0.0252759684290393+0.04377926153004382j)
1 -1 1 F: (5.256447111893667e-20-3.034811155032838e-20j) E: (0.18448308813935999-1.99618918815216e-29j) V: (-0.16913060635758062-0.2929428033292114j) (0.33826121271771603+1.474920100812128e-12j)
1 -1 -1 F: (5.256447111893667e-20-3.034811155032838e-20j) E: (0.18448308813935999-1.99618918815216e-29j) V: (-0.16913060635758062-0.2929428033292114j) (0.33826121271771603+1.474920100812128e-12j)
-1 1 1 F: (2.4398266219041667e+17+1.4086345569323858e+17j) E: (0.09269011940029581-1.996147115210449e-17j) V: (0.0505519368584612-2.2039674490864953e-13j) (-0.02527596842903972+0.04377926153004451j)
-1 1 -1 F: (2.4398266219041667e+17+1.4086345569323858e+17j) E: (0.09269011940029581-1.996147115210449e-17j) V: (0.0505519368584612-2.2039674490864953e-13j) (-0.02527596842903972+0.04377926153004451j)
-1 -1 1 F: (5.256447111893667e-20-3.034811155032838e-20j) E: (0.18448308813935999-1.024086860531348e-17j) V: (-0.1691306063575802-0.2929428033292107j) (0.3382612127177152+1.474944404825014e-12j)
-1 -1 -1 F: (5.256447111893667e-20-3.034811155032838e-20j) E: (0.18448308813935999-1.024086860531348e-17j) V: (-0.1691306063575802-0.2929428033292107j) (0.3382612127177152+1.474944404825014e-12j)

0.520876591889109 / 0.2840790448279948

1.8335621770500221

val = s_inv2(1e55 - 1e-55j)
np.atan2(val.imag, val.real) / np.pi

np.float64(0.33333333333194537)

1 / (1728) ** (1 / 5)

0.2251600064201022

val23 / val12

np.float64(1.392382021468321)

theta = np.arccos((1 + np.sqrt(5)) / 2 / np.sqrt(3))
val23 = np.cos(theta) / (1 + np.sin(theta))
val23

np.float64(0.6885002580691648)

alpha = np.arccos(1 / 2 / np.sin(np.pi / 5))
theta = np.arccos((1 + np.sqrt(5)) / 2 / np.sqrt(3) * np.cos(alpha))
val12 = np.cos(theta) / (1 + np.sin(theta))
val12

np.float64(0.49447654986460865)

import matplotlib.pyplot as plt

exps = np.linspace(-20, 0, 100)
exps = exps
xs = np.pow(10, exps)
print(xs)
ys = s_inv(xs)
print(ys)
plt.scatter(xs, ys)
plt.xscale("log")
plt.show()

[1.00000000e-20 1.59228279e-20 2.53536449e-20 4.03701726e-20
 6.42807312e-20 1.02353102e-19 1.62975083e-19 2.59502421e-19
 4.13201240e-19 6.57933225e-19 1.04761575e-18 1.66810054e-18
 2.65608778e-18 4.22924287e-18 6.73415066e-18 1.07226722e-17
 1.70735265e-17 2.71858824e-17 4.32876128e-17 6.89261210e-17
 1.09749877e-16 1.74752840e-16 2.78255940e-16 4.43062146e-16
 7.05480231e-16 1.12332403e-15 1.78864953e-15 2.84803587e-15
 4.53487851e-15 7.22080902e-15 1.14975700e-14 1.83073828e-14
 2.91505306e-14 4.64158883e-14 7.39072203e-14 1.17681195e-13
 1.87381742e-13 2.98364724e-13 4.75081016e-13 7.56463328e-13
 1.20450354e-12 1.91791026e-12 3.05385551e-12 4.86260158e-12
 7.74263683e-12 1.23284674e-11 1.96304065e-11 3.12571585e-11
 4.97702356e-11 7.92482898e-11 1.26185688e-10 2.00923300e-10
 3.19926714e-10 5.09413801e-10 8.11130831e-10 1.29154967e-09
 2.05651231e-09 3.27454916e-09 5.21400829e-09 8.30217568e-09
 1.32194115e-08 2.10490414e-08 3.35160265e-08 5.33669923e-08
 8.49753436e-08 1.35304777e-07 2.15443469e-07 3.43046929e-07
 5.46227722e-07 8.69749003e-07 1.38488637e-06 2.20513074e-06
 3.51119173e-06 5.59081018e-06 8.90215085e-06 1.41747416e-05
 2.25701972e-05 3.59381366e-05 5.72236766e-05 9.11162756e-05
 1.45082878e-04 2.31012970e-04 3.67837977e-04 5.85702082e-04
 9.32603347e-04 1.48496826e-03 2.36448941e-03 3.76493581e-03
 5.99484250e-03 9.54548457e-03 1.51991108e-02 2.42012826e-02
 3.85352859e-02 6.13590727e-02 9.77009957e-02 1.55567614e-01
 2.47707636e-01 3.94420606e-01 6.28029144e-01 1.00000000e+00]
[       nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan        nan        nan        nan
        nan        nan        nan 0.28407904]

/var/folders/8g/byx83mzd7gz503xq8dj4cjr40000gp/T/ipykernel_65992/594549837.py:19: RuntimeWarning: invalid value encountered in divide
  return coeff * np.divide(num , denom)

_images/2bd7e31c32bbc977409ae09c28e1b6ad1330ab280fbfaeedd1679b4e82e7da28.png

for s1, s2, s3, exp in product([+1, -1], [+1, -1], [+1, -1], [0, 1, oo]):
    get_soln(1, 1, 1, oo)(-1e-55 * I)

from sympy import I, exp, pi

expr = get_soln(1, 1, 1, oo)(z)
(expr.subs(z, -0.000000001 - 0.00000000 * I) * exp(-I * pi / 5)).evalf()

0.104483432712088 - 0.321566940765553 i

c = _
s = symbols("s")
solve(c / s ** (1 / 5) - 0.284079043840412, s)

[]

alpha = np.arccos(1 / 2 / np.sin(np.pi / 5))
n3 = (
    2
    / np.sqrt(3)
    * np.array(
        [
            -np.sin(alpha) * np.cos(np.pi / 5),
            np.sin(alpha) * np.sin(np.pi / 5),
            np.cos(alpha) * np.cos(np.pi / 5),
        ]
    )
)
n2 = np.array([-np.sin(alpha), 0, np.cos(alpha)])
dp = np.dot(n2, n3)
print(dp)
cp = np.cross(n2, n3)
theta = np.arccos(dp)
yp = cp / np.sin(theta)
# xp = (n2 - dp*n3)/np.sqrt(2*(1-dp**2))
np.linalg.norm(yp), np.linalg.norm(n3), np.linalg.norm(n2)

0.9341723589627158

(np.float64(1.000000000000001),
 np.float64(1.0000000000000002),
 np.float64(1.0))

xp = np.cross(yp, n3)
np.linalg.norm(yp)

np.float64(1.000000000000001)

xp, yp, n3

(array([ 0.18759247,  0.93417236, -0.303531  ]),
 array([-0.85065081,  0.        , -0.52573111]),
 array([-0.49112347,  0.35682209,  0.79465447]))

O = np.vstack((xp, yp, n3))
O

array([[ 0.18759247,  0.93417236, -0.303531  ],
       [-0.85065081,  0.        , -0.52573111],
       [-0.49112347,  0.35682209,  0.79465447]])

zp = O @ np.array([0, 0, 1])
zp

array([-0.303531  , -0.52573111,  0.79465447])

zp = -zp
zpz = (zp[0] + I * zp[1]) / (1 - zp[2])
zpz

0.169130606358858 + 0.292942803328475 i

(zpz * exp(-I * pi / 3)).evalf()

0.338261212717717 - 6.29921462214078 \cdot 10^{- 17} i

n2p = O @ n2
n2p = -n2p
n2pz = (n2p[0] + I * n2p[1]) / (1 - n2p[2])
n2pz

0.184483088138253 - 2.87002091483864 \cdot 10^{- 17} i

O @ n3, O @ n2

(array([5.55111512e-17, 5.55111512e-17, 1.00000000e+00]),
 array([-3.56822090e-01,  5.55111512e-17,  9.34172359e-01]))

-n3p[0] / (1 + n3p[2])

np.float64(0.1252004517810262)

(1 + np.sqrt(5)) / 2 / np.sqrt(3)

np.float64(0.9341723589627158)

u, v, z, z_n = symbols("u v z z_n")

f = u * v * (u**10 + 11 * u**5 * v**5 - v**10)
H = (
    u**30
    + 522 * (u**25 * v**5 - u**5 * v**25)
    - 10005 * (u**20 * v**10 - u**10 * v**20)
    + v**30
)
F = u**20 - 228 * (u**15 * v**5 - u**5 * v**15) + 494 * u**10 * v**10 + v**20

from utils import z_simp

num = z_simp((F**3).subs(u, z * z_n + 1).subs(v, z - z_n).expand(), z_n)
num

15693023681640625 z^{60} - 10734028198242187500 z^{55} + 2470615490295410156250 z^{50} - 196593726450805664062500 z^{45} + 1215589382426605224609375 z^{40} - 2050907831725341796875000 z^{35} - 521195509844848632812500 z^{30} + 2050907831725341796875000 z^{25} + 1215589382426605224609375 z^{20} + 196593726450805664062500 z^{15} + 2470615490295410156250 z^{10} + 10734028198242187500 z^{5} + z_{n} (- 25391845703125000 z^{60} + 17368022460937500000 z^{55} - 3997539836425781250000 z^{50} + 318095331372070312500000 z^{45} - 1966864937127685546875000 z^{40} + 3318438579521484375000000 z^{35} + 843312049711914062500000 z^{30} - 3318438579521484375000000 z^{25} - 1966864937127685546875000 z^{20} - 318095331372070312500000 z^{15} - 3997539836425781250000 z^{10} - 17368022460937500000 z^{5} - 25391845703125000) + 15693023681640625

_ / 15693023681640625

z^{60} - 684 z^{55} + 157434 z^{50} - 12527460 z^{45} + 77460495 z^{40} - 130689144 z^{35} - 33211924 z^{30} + 130689144 z^{25} + 77460495 z^{20} + 12527460 z^{15} + 157434 z^{10} + 684 z^{5} + \frac{z_{n} (- 25391845703125000 z^{60} + 17368022460937500000 z^{55} - 3997539836425781250000 z^{50} + 318095331372070312500000 z^{45} - 1966864937127685546875000 z^{40} + 3318438579521484375000000 z^{35} + 843312049711914062500000 z^{30} - 3318438579521484375000000 z^{25} - 1966864937127685546875000 z^{20} - 318095331372070312500000 z^{15} - 3997539836425781250000 z^{10} - 17368022460937500000 z^{5} - 25391845703125000)}{15693023681640625} + 1

denom = z_simp((f**5).subs(u, z * z_n + 1).subs(v, z - z_n).expand(), z_n)
denom

15693023681640625 z^{55} + 863116302490234375 z^{50} + 18910093536376953125 z^{45} + 205421679992675781250 z^{40} + 1091999052886962890625 z^{35} + 2114807564361572265625 z^{30} - 1091999052886962890625 z^{25} + 205421679992675781250 z^{20} - 18910093536376953125 z^{15} + 863116302490234375 z^{10} - 15693023681640625 z^{5} + z_{n} (- 25391845703125000 z^{55} - 1396551513671875000 z^{50} - 30597174072265625000 z^{45} - 332379260253906250000 z^{40} - 1766891583251953125000 z^{35} - 3421830518798828125000 z^{30} + 1766891583251953125000 z^{25} - 332379260253906250000 z^{20} + 30597174072265625000 z^{15} - 1396551513671875000 z^{10} + 25391845703125000 z^{5})

z_simp(denom * denom.subs(z_n, -1 - z_n), z_n)

931322574615478515625 z^{10} {(z^{2} + z - 1)}^{10} {(z^{4} - 3 z^{3} + 4 z^{2} - 2 z + 1)}^{10} {(z^{4} + 2 z^{3} + 4 z^{2} + 3 z + 1)}^{10}

(f**5).subs(u, z).subs(v, 1).factor()

z^{5} {(z^{2} + z - 1)}^{5} {(z^{4} - 3 z^{3} + 4 z^{2} - 2 z + 1)}^{5} {(z^{4} + 2 z^{3} + 4 z^{2} + 3 z + 1)}^{5}

z_simp(num * denom.subs(z_n, -1 - z_n), z_n)

931322574615478515625 z^{115} - 585801899433135986328125 z^{110} + 112707726657390594482421875 z^{105} - 4358328878879547119140625000 z^{100} - 401144670322537422180175781250 z^{95} - 8337759913876652717590332031250 z^{90} - 62401286315172910690307617187500 z^{85} + 4024955218657851219177246093750 z^{80} + 1813690744242630898952484130859375 z^{75} + 1811835736907087266445159912109375 z^{70} - 22046607219167985022068023681640625 z^{65} + 14687385724041610956192016601562500 z^{60} + 22046607219167985022068023681640625 z^{55} + 1811835736907087266445159912109375 z^{50} - 1813690744242630898952484130859375 z^{45} + 4024955218657851219177246093750 z^{40} + 62401286315172910690307617187500 z^{35} - 8337759913876652717590332031250 z^{30} + 401144670322537422180175781250 z^{25} - 4358328878879547119140625000 z^{20} - 112707726657390594482421875 z^{15} - 585801899433135986328125 z^{10} - 931322574615478515625 z^{5}

(931322574615478515625 * F**3 * f**5).subs(u, z).subs(v, 1).expand()

931322574615478515625 z^{115} - 585801899433135986328125 z^{110} + 112707726657390594482421875 z^{105} - 4358328878879547119140625000 z^{100} - 401144670322537422180175781250 z^{95} - 8337759913876652717590332031250 z^{90} - 62401286315172910690307617187500 z^{85} + 4024955218657851219177246093750 z^{80} + 1813690744242630898952484130859375 z^{75} + 1811835736907087266445159912109375 z^{70} - 22046607219167985022068023681640625 z^{65} + 14687385724041610956192016601562500 z^{60} + 22046607219167985022068023681640625 z^{55} + 1811835736907087266445159912109375 z^{50} - 1813690744242630898952484130859375 z^{45} + 4024955218657851219177246093750 z^{40} + 62401286315172910690307617187500 z^{35} - 8337759913876652717590332031250 z^{30} + 401144670322537422180175781250 z^{25} - 4358328878879547119140625000 z^{20} - 112707726657390594482421875 z^{15} - 585801899433135986328125 z^{10} - 931322574615478515625 z^{5}

z_simp(num * denom.subs(z_n, -1 - z_n), z_n).expand().equals(
    (931322574615478515625 * F**3 * f**5).subs(u, z).subs(v, 1).expand()
)

True

_ / 15693023681640625

z^{55} + 55 z^{50} + 1205 z^{45} + 13090 z^{40} + 69585 z^{35} + 134761 z^{30} - 69585 z^{25} + 13090 z^{20} - 1205 z^{15} + 55 z^{10} - z^{5} + \frac{z_{n} (- 25391845703125000 z^{55} - 1396551513671875000 z^{50} - 30597174072265625000 z^{45} - 332379260253906250000 z^{40} - 1766891583251953125000 z^{35} - 3421830518798828125000 z^{30} + 1766891583251953125000 z^{25} - 332379260253906250000 z^{20} + 30597174072265625000 z^{15} - 1396551513671875000 z^{10} + 25391845703125000 z^{5})}{15693023681640625}

25391845703125000 / 15693023681640625

1.6180339887482036